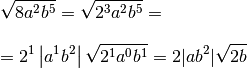A radical simplification

To radically simplify, you must divide the index of the root and the exponents of the factors of the radicand by their possible common divisor, and then take out the factors that have an exponent greater than or equal to the index of the root.

The radical obtained by simplification is called a radical in normal form .

Let’s try to be more precise and list the steps that need to be followed in order to correctly simplify the radical.

• Find the conditions for the existence of a radical.

• Factor all the numerical factors present under the root into prime numbers.

• Calculate the greatest common divisor (gcd) between the root index and the exponents of all factors of the radicand:

– if gcd is other than 1, divide the index of the root and all exponents by the calculated gcd and go to the next point;

– if gcd is equal to 1, go directly to the next point.

• Identify radicand factors with an exponent greater than or equal to the root index.

• Divide each exponent greater than equal to the index of the root by the index itself:

– the division quotient is the exponent of the factor, which must be written outside the root;

– the remainder of the division is the exponent of the factor that remains in the root.

• If the root index is an even number, put the absolute value in the variable quantities (letters) taken from the root.

• Subtract the absolute value from quantities that are definitely not negative.

The end!

Examples for simplifying radicals

1)

Implementation : first we observe that the radical is defined for every because the index of the root is an odd number and the radicand has no terms that require existence conditions.

We decompose the numerical factor (27) into prime factors

and we get

We calculate the greatest common divisor between the root index (9) and the exponents of the radicand factors (3, 3, 6)

Since gcd is different from 1, we divide the root index and various exponents by gcd

The exponents of the new radicand factors are all less than the root index, so we don’t need to do anything else.

2)

Implementation : first we observe that the radical is defined for in fact the index of the root is even and the radicand consists of factors:

• which is a positive quantity;

• which is a non-negative quantity for every possible value ;

• which is a nonnegative quantity if and only if .

Then we decompose the numerical factor into prime factors:

Then

We then calculate the gcd between the index of the root and the exponents of the factors under the root

Since it is equal to 1, we can proceed further.

We observe that all three factors have an exponent greater than or equal to the root index, so we divide between each exponent and the index.

therefore a factor of 2 will have an exponent of 1 both inside and outside the root.

thus the factor will have an exponent of 1 outside the root and an exponent of 0 inside the root.

thus the factor will have an exponent of 2 outside the root and an exponent of 1 inside.

Now we can simplify the radical, not forgetting to place the variable quantities, i.e. the letters, between the absolute value of A

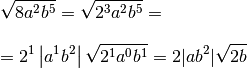
Finally, since it is definitely not a negative quantity, we can remove it from the absolute value and conclude that:

3)

Execution : in terms of the conditions of existence that we must impose

in fact, the root index is even and the base is raised to an odd exponent (if it was also a power it will be negative).

We decompose the numerator and denominator of a single numerical factor of the radicand into prime factors

and we rewrite the radical as follows

We find the greatest common divisor between the index and the exponents

Since it is equal to 3, we divide the index of the square root and the various exponents by 3

The exponent is greater than the index of the root, so we need to carry out the transfer outside the root.

We divide between the exponent and the root index (2)

and we get this factor will have an exponent of 2 outside the root and an exponent of 1 inside the root.

Similarly for the factor

Definitely: