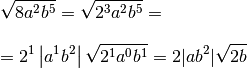In this note we see what the incenter of a triangle consists of and what its properties are. In order to fully understand the contents of this note it is necessary to be familiar with the concepts of triangle and angle bisector. In particular in this note we will see:
For further notes on plane geometry we refer you to the relevant index of topics. For further notes on analytical geometry we refer you to the relevant index.
Definition of incenter of a triangle
An important property of triangles is that:
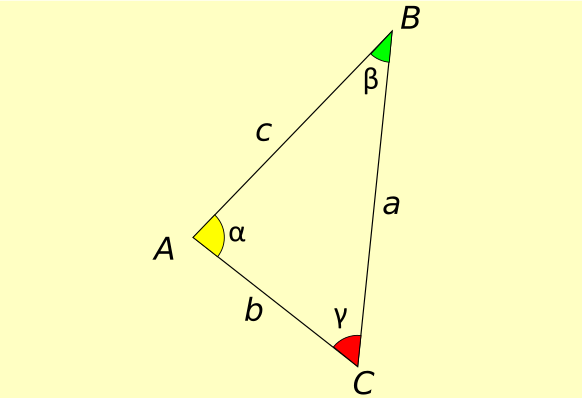
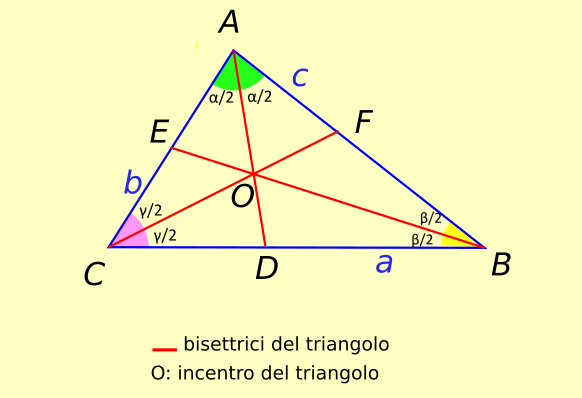
The bisectors of the internal angles of a triangle intersect at a point inside it called the incenter of the triangle
This property is valid for any type of triangle. Let’s see in the next paragraph what the main properties of this point are.
Ownership of the center
Let’s see some properties of this point below:
-
- It is a point always inside the triangle, whatever the type of triangle
-
- It coincides with the center of the circumference inscribed in the triangle
- It is equidistant from three sides. This property derives from the previous property. In fact the sides are tangent to the circumference inscribed on the triangle. As such the radius of the circle coincides with the distance of the center of the circle from each of the three sides. Since the center of the circle coincides with the incenter, it follows that the incenter is distant from each side by a distance equal to the radius of the inscribed circle
-
- In an equilateral triangle the incenter coincides with the barycenter, the circumcenter and the orthocenter.
-
- The incenter divides each bisector into two parts. These parts are proportional to each other exactly as are the other two sides of the two triangles into which the original triangle is divided by the bisector.
Let us better describe this last property of the center. Let’s consider the triangle ABC:
This property tells us that the bisector AD divides the triangle ABC into two triangles having in common the bisector AD as their side: ABD and ACD. The property tells us that:
Similarly we have for the bisector BE:
and for the bisector CF:
In-centre demonstration
Proving that all bisectors of a generic triangle meet at a single point is quite simple. The bisector of an angle by definition is the locus of the points equidistant from the two segments that make up the angle. We therefore draw the bisector AD and BE of the triangle. The meeting point O will be equidistant from side AB and side AC as it belongs to the bisector AD. Since O also belongs to the bisector BE, then it will be equidistant from the sides AB and BC. It follows that O is equidistant from sides BC and AC. This implies that O also belongs to the bisector CF.
Since the point O is equidistant from the three sides, it will be possible to draw a circle having the incenter as its center and the distance of the incenter from the three sides as its radius. This circumference is the inscribed circle.
