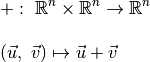Applied Maths

Operations between carriers

By admin

In this lesson, we deal with the operations of sum and difference between vectors and the product of a vector using a scalar, working in R^n. As special cases, we will consider the plane and space, marked respectively R^2A, R^3where the operations of sum and difference between vectors can also be solved geometrically using the parallelogram rule or the tip-to-tail method.

For each operation, we give a definition, list various properties, and show some examples explaining how the parallelogram rule and the endpoint method are applied to plane and space vectors. If you haven’t already done so, we recommend that you check out our lesson on vectors before you start.

Sum and difference between vectors

u = (u_1, u_2, ..., u_n)Let A be v = (v_1, v_2, ..., v_n)two vectors R^n.

1) There, the sum between vectors is an internal operation

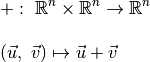
+: R^n×R^n → R^n; (u, v) ↦ u+v

which joins the vectors uA againsta new vector, said sum vector whose components are given by the sum of the components of z uand zagainst

u+v = (u_1+v_1, u_2+v_2, ..., u_n+v_n)

2) Operation difference between vectors is a law that is related to vectorsuAagainstThe difference vector u-v whose components are given by the difference of the respective components.

u−v = (u_1−v_1, u_2−v_2, ..., u_n−v_n)

An example of the sum and difference of vectors

Calculate the sum and difference of the vectors

u = (1,-5, 7, 4); v = (−2, 8,−12, 3)

Design :

u+v = (u_1+v_1, u_2+v_2, u_3+v_3, u_4+v_4) = (1+(−2), −5+8, 7+(−12), 4+3) = (−1 , 3, -5, 7); u−v = (u_1−v_1, u_2−v_2, u_3−v_3, u_4−v_4) = (1−(−2), −5−8, 7−(−12), 4−3) = (3, −13, 19, 1)

Algebraic sum of vectors

It is customary to define the difference between two vectors uA againstas the sum uand inverse of against. In symbols

u−v = u+(−v)

Where −vit has as components the opposites of the components, againstso to speak, the components againstchange sign.

The difference between vectors is thus nothing but a sum, and it is for this reason that we do not speak of a sum and a difference, but simply of an algebraic sum between vectors.

Graphical methods for sum and difference between vectors

We now describe two methods by which it is possible to graphically identify the sum vector and the difference vector associated with two aircraft or space uA vectors against.

Parallelogram rule

Let them be {AB}the representative of the carrier uAND {CD}the representative of the carrier against.

To find the sum vector u+vand the difference vector u-vwith the parallelogram rule, proceed as follows:

– by moving (which leaves the module, direction and direction unchanged) we move the oriented segment {CD}so that its origin Ccoincides with the origin THATof the oriented segment {AB};

– we construct a parallelogram that has two segments as sides ABA CD.

The sum vector is a directed segment {AE}while the difference vector is {DB}each of which coincides with a diagonal of the parallelogram from which the name of this graphical method derives.

Parallelogram rule

Sum and difference of two vectors with the parallelogram rule

Tip-tail metoda

Before we talk to you about the tip-to-tail method, it is good to clarify that the tail of the applied vector is its point of application, while by tip we mean its final end, which corresponds to the tip of the arrow.

uLet A be againsttwo vectors of a plane or space.

To determine the sum vector by the tip-to-tail method, we must translate the vector againstso that its tail coincides with the tip u.

The vector sums u+vthat is what joins the tail uwith the tip against.

Tip-tail metoda

The sum of two vectors using the tip-tail method.

To find the difference vector, we need to find the opposite of the vector againstwhich has the same magnitude and the same direction as againstbut in the opposite direction and proceed in the same way using the vectors uA −v.

The sum property between vectors

Below we have given the properties of the algebraic sum between vectors, which implies with u, v, wany three vectors R^nwith nany.

1) Commutative property

u+v = v+u

2) Associative property

u+(v+w) = (u+v)+w

3) Neutral element: the zero vector 0 acts as a neutral element of the sum, i.e.

v+0 = v = 0+v

4) Existence of the opposite: for every vectoragainstthere is one and only one vector, called opposite to Zagainstit is implied−vthat

v+(−v) = 0 = −v+v

For those who studied university algebra, these properties allow us to state that (R^n,+)they are a commutative group, also known as an Abelian group .

The product of a vector and a scalar

Let them be λ ∈ Ra real number, which from now on we will call rise A v = (v_1, v_2, ..., v_n)vector R^n.

The product of a scalar and a vector is an external operation

R×R^n → R^n; (λ, v) ↦ λ v

than (λ, v)associates to the pair a new vector whose components are obtained by multiplying each againstclimbing component by l.

λ v = λ(v_1, v_2, ..., v_n) = (λ v_1, λ v_2, ..., λ v_n)

An example of the product of a vector by a scalar

Let them be v = (−1, 3, 5,−9) a λ = −2. Calculate the product of the vector againstand the climb l.

Design :

λ v = −2(−1, 3,5,−9) = (−2(−1), −2(3), −2(5), −2(−9)) = (2,−6 ,−10,18)

A geometric method for the product of a vector and a scalar

I againstis a plane or space vector other than the zero vector, the againstclimbing product of lA:

– zero vector ifλ = 0

If not, then if λ ≠ 0, λ vis a vector that has:

— direction : same as vector against;

— against : the same as againstme λ > 0, the opposite of againstme λ < 0;

— modulus : given by the product of the absolute value lfor the form againstor:

||λ v|| = |λ| ||v||

Product property of a vector and a scalar

We will end this lesson by communicating the properties of the product operation of a vector using a scalar, where we have indicated with lA many two scalars and with uevtwo generic vectors R^n.

1) Distributive property of the product with respect to the sum between vectors:

λ (u+v) = λ u+λ v

2) Distribution property of the product with respect to the sum of scalars:

(λ+μ) v = λ v+μ v

3) Properties of homogeneity

λ (μ v) = (λ μ) v

4) Existence of a neutral element:

1 v = v

 

Related Posts

Applied Maths

A radical simplification

By admin
Applied Maths

Triangle: Definition and Classification

By admin

Leave a Reply

Your email address will not be published. Required fields are marked *