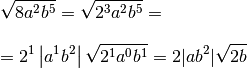In this note we see what the orthocenter of a triangle consists of and its properties. To fully understand the contents of this note we recommend being familiar with the concepts of triangle, height of a triangle and classification of angles. In particular in this note we will see:
For further notes on plane geometry we refer you to the relevant index of topics.
Definition of orthocenter of a triangle
The orthocenter of a triangle is the meeting point of the altitudes or their extensions of a triangle.
This definition provides us with two important concepts. The first is that the orthocenter is related to the concept of the height of a triangle. We know that for each triangle it is possible to define 3 heights. Each height is the segment that joins a vertex to the opposite side or to its projection.
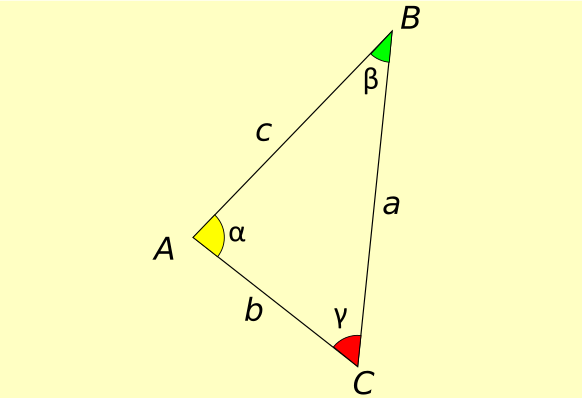
The second very important concept is that the three heights or their extensions of a triangle meet at the same point and this point is called the orthocenter. Let’s see an example below:
- AH is the height relative to side BC of the triangle
-
- BI is the height relative to side AC of the triangle
-
- CL is height relative to side AB
they, as expected, all three meet at the same point O. In the next paragraph we will see what the main properties of the orthocenter are:
Properties of the orthocenter
There position of the orthocenter depends on the type of triangle. To understand this concept let’s look at the following figure:
the first triangle represented is an acute-angled triangle, i.e. a triangle having all acute internal angles (angles less than 90° sexagesimal). In this case we observe that the position of the orthocenter is inside the triangle. The second triangle is an obtuse triangle. Here the orthocenter is outside the triangle. The third triangle is a right-angled triangle. In this case the vertex on which the right angle lies coincides with the base of the heights relating to the two legs and consequently coincides with the orthocenter of the triangle.
So, in summary we can derive the following general rule:
-
- If the orthocenter is internal, then the triangle is acute-angled
-
- When the orthocenter is external, then the triangle is obtuse
-
- If the orthocenter coincides with a vertex of the triangle, then this triangle will be a right triangle
Also note that:
-
- There is no triangle in which the orthocenter is positioned on one of the sides without coinciding with a vertex
Another property of the orthocenter is that:
-
- in an isosceles triangle, the orthocenter coincides with the centroid and the incenter of the triangle.
Demonstration
We now prove that the altitudes of a triangle meet at a common point. Let’s consider a generic triangle ABC:
we draw on each vertex the line parallel to the opposite side. The three lines meet two by two at a point constituting a new triangle which we will indicate with the letters A’B’C’:
note that the quadrilateral ABCB’ is a parallelogram and as such the sides BC and AB’ are congruent with each other. Similarly the quadrilateral AC’BC is also a parallelogram. As such the sides BC and AC’ are also congruent. It therefore follows that AB’ is congruent to AC’ and consequently A is the midpoint of B’C’. The same proof can be performed for the other two vertices. It will result that:
B is the midpoint of A’C’ and C is the midpoint of A’B’. Now we trace the height from A to side BC:
Now note that since the line passing through AH is perpendicular to BC, it will also be perpendicular to B’C’. Since it also passes through the midpoint of B’C’, then the straight line passing through AH is also the median of the side B’C’.
If we extend the reasoning also to the vertices B and C we obtain the medians of A’C’ and A’B’. Therefore we have the three medians of the triangle A’B’C’. But we know that the three medians of a triangle meet at a point called the circumcenter:
But the three medians of A’B’C’ are the heights of ABC. Therefore, proving that the 3 medians of A’B’C’ meet in a point means proving that the three heights of ABC meet in a point 
