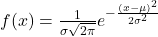Basic Statistics

Expected value and Variance

By admin

In this note we will see what they are and how to obtain them the expected value And the variance from the normal distribution. To fully understand the content of this note it is necessary to know the definition of these two mathematical operators which you can find in detail at the following links (link1, link2). An introduction to the normal distribution, with the description of its characteristics and key statistical properties, can be found at the following link. So in this note you will see:

For further notes and statistics topics you can click on the following link or use the search bar at the top.

Calculation of the expected value

We demonstrate with all the mathematical steps the expected value of the normal distribution, whose mathematical function is the following:

f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}}

We calculate the expected value by applying the definition of the same in the case of a continuous variable distribution:

E(x)= \int_{-\infty}^{+\infty}xf(x) dx =\int_{-\infty}^{+\infty}x\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx

to solve the integral we proceed by applying change of variable:

t = \frac{x-\mu}{\sqrt{2}\sigma}\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,x=\sqrt{2}\sigma t + \mu \,\,\,\,\,\, \Rightarrow \,\,\,\,\,\, dx = \sqrt{2}\sigma dt

the integral then becomes:

E(x) = \frac{\sqrt{2} \sigma}{\sigma \sqrt{2\pi}}\int^{+\infty}_{-\infty} (\sqrt{2}\sigma t +\mu)e^{-t^{2}}dt =\frac{1}{\sqrt{\pi}} \left(\sqrt{2}\sigma\int^{+\infty}_{-\infty}te^{-t^{2}}dt+\mu\int^{+\infty}_{-\infty}e^{-t^{2}}dt\right)

note that the second term is nothing other than the Gauss integral:

\int^{+\infty}_{-\infty}e^{-t^{2}}dt = \sqrt{\pi}

So we can rewrite everything:

E(x) = \frac{1}{\sqrt{\pi}} \left(\sqrt{2}\sigma \left(-\frac{1}{2}e^{-t^{2}}\right)_{-\infty}^{+\infty}+\mu\sqrt{\pi}\right)

but the obtained exponential function tends to zero both at minus infinity and at + infinity. So only the second term in brackets remains:

E(x)= \frac{\mu \sqrt{\pi}}{\sqrt{\pi}} = \mu

We have therefore demonstrated that the expected value of the normal distribution is equal to mu, i.e. at its center.

Calculation of the variance of the normal distribution

To calculate the variance of the normal distribution, we start from its definition:

V(x) = E(x^{2})- E(x)^{2}

the expected value E(x) was calculated in the previous paragraph. Let us now calculate the expected value of the square of x:

E(x^{2}) = \int_{-\infty}^{+\infty} x^{2} \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^{2}}{2\sigma ^{2}}}dx

Let’s immediately perform a change of variable:

t= \frac{x-\mu}{\sqrt{2}\sigma} \\\,\\ \,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,\, \\\,\\ x=\sqrt{2}\sigma t+\mu \\\,\\ \,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,\, \\\,\\ dx=\sqrt{2}\sigma dt

so let’s rewrite the integral:

E(x^{2}) = \int_{-\infty}^{+\infty} x^{2} \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^{2}}{2\sigma ^{2}}}dx = \\\,\\ =\frac{\sigma \sqrt{2}}{\sigma \sqrt{2\pi}}\int_{-\infty}^{+\infty} (\sqrt{2}\sigma t+\mu)^{2} e^{-t^{2}}dt= \\\,\\ = \frac{1}{\sqrt{\pi}} \left(2\sigma^{2}\int_{-\infty}^{+\infty} t^{2}  e^{-t^{2}}dt+2\sigma\sqrt{2}\int_{-\infty}^{+\infty}t  e^{-t^{2}}dt+\mu^{2}\int_{-\infty}^{+\infty}  e^{-t^{2}}dt \right)

but some of these integrals are known. Like the Gauss integral:

\int_{-\infty}^{+\infty}e^{-t^{2}dt} = \sqrt{\pi}

while we can easily solve:

\int_{-\infty}^{+\infty}te^{-t^{2}dt} = \left(-\frac{1}{2}e^{-t^{2}}\right)^{+\infty}_{-\infty} = 0-0=0

To solve the last integral (the first in the bracket) we must operate an integration by parts:

2\sigma^{2} \int_{-\infty}^{+\infty}t^{2}e^{-t^{2}}dt = 2\sigma^{2} \left( -\frac{t}{2}e^{-t^{2}}\right)_{-\infty}^{+\infty}+\sigma^{2}\int_{-\infty}^{+\infty}e^{-t^{2}}dt = \sigma^{2}\int_{-\infty}^{+\infty}e^{-t^{2}}dt = \sigma^{2}\sqrt{\pi}

we replace these three integrals in the formula. We obtain::

E(x^{2}) = \frac{1}{\sqrt{\pi}} \left(2\sigma^{2}\int_{-\infty}^{+\infty} t^{2}  e^{-t^{2}}dt+2\sigma\sqrt{2}\int_{-\infty}^{+\infty}t  e^{-t^{2}}dt+\mu^{2}\int_{-\infty}^{+\infty}  e^{-t^{2}}dt \right) =\\\,\\= \frac{1}{\sqrt{\pi}} \left(\sigma^{2}\sqrt{\pi}+0+\mu^{2}\sqrt{\pi} \right)  = \sigma^{2}+\mu^{2}

Let’s now calculate the variance:

V(x) = E(x^{2})-E(x)^{2} = \sigma^{2}+\mu^{2}-\mu^{2} = \sigma^{2}

Related Posts

Basic Statistics

Basic Statistics for reliability and mortality concepts

By admin
Basic Statistics

Poisson distribution: expected value and variance

By admin

Leave a Reply

Your email address will not be published. Required fields are marked *