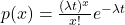Poisson distribution: expected value and variance

In this note we will see what they are and how to obtain them the expected value And the variance from the Poisson distribution. To properly understand the content of this note it is necessary to know the definition of these two mathematical operators which you can find at the following links (link1, link2). The definition of Poisson distribution can be found at the following link. So in this note you will see:

For further notes and statistics topics you can click on the following link or use the search bar at the top.

Expected value of the Poisson distribution

The Poisson distribution is a discrete variable distribution, used to describe the probability that x events of a certain type can occur knowing that the number of events that occur in a given interval t is equal to lambda. The distribution therefore has the following form:

p(x) = \frac{(\lambda t)^{x}}{x!}e^{-\lambda t}

We calculate the expected value using its definition:

E(x) = \sum_{x_{i}=0}^{\infty} x_{i} p(x_{i})

it therefore follows that:

E(x)= \sum_{x_{i}=0}^{\infty} x_{i} \frac{(\lambda t)^{x_{i}}}{x_{i}!}e^{-\lambda t} =\sum_{x_{i}=0}^{\infty} \frac{(\lambda t)^{x_{i}}}{(x_{i}-1)!}e^{-\lambda t}

now we can take the lambda constant term for t and the exponential term out of the summation:

E(x) =\sum_{x_{i}=0}^{\infty} \frac{(\lambda t)^{x_{i}}}{(x_{i}-1)!}e^{-\lambda t} = \lambda t e^{-\lambda t}\sum_{x_{i}=0}^{\infty} \frac{(\lambda t)^{(x_{i}-1)}}{(x_{i}-1)!}

Let’s now perform a change of variable: s=x_the-1:

E(x) = \lambda t e^{-\lambda t}\sum_{s=1}^{\infty} \frac{(\lambda t)^{(s)}}{s!}

but the summation is nothing other than the Taylor series of the exponential function:

e^{\lambda t} = \sum_{s=1}^{\infty} \frac{(\lambda t)^{(s)}}{s!}

Therefore the expected value becomes:

E(x) = \lambda t e^{-\lambda t}\sum_{s=1}^{\infty} \frac{(\lambda t)^{(s)}}{s!} = \lambda t e^{-\lambda t}e^{\lambda t} =\lambda t

It is therefore demonstrated that the expected value of the Poisson distribution is precisely equal to the product of lambda and time

Variance of the Poisson distribution

Let us now calculate the variance of the Poisson distribution. To do this we use the definition of variance:

Having demonstrated the expected value of the Poisson distribution in the previous paragraph, all we have to do is calculate the expected value of x squared: